Relations entre l'ellipsoïde des indices et les éléments de symétrie
Comme toutes les propriétés du cristal, les propriétés optiques doivent respecter les éléments de symétrie. Les éléments de symétrie de l'ellipsoïde doivent donc correspondre aux éléments de symétrie du cristal.

Si le cristal est du système cubique, il présente alors plusieurs axes de symétrie supérieurs, la seule solution est donc que l'ellipsoïde des indices soit une sphère. Le cristal du système cubique est donc isotrope du point de vue des propriétés optiques. Tous les minéraux du système cubique sont isotropes;
Si le cristal présente au moins un élément de symétrie d'ordre supérieur (\(A3\), \(A4\) ou \(A6\)), l'ellipsoïde des indices est un ellipsoïde de révolution et l'axe infini correspond à l'axe de symétrie d'ordre supérieur. Les cristaux des systèmes rhomboédrique, quadratique et hexagonal sont des uniaxes.
Position de l'indicatrice dans le système quadratique

Position de l'indicatrice dans le système hexagonal

Position de l'indicatrice dans le système rhomboédrique

Si l'ellipsoïde n'admet que des \(A2\), et/ou des \(M\) ou un \(C\), le cristal appartient aux systèmes orthorhombique, monoclinique ou triclinique.
L'ellipsoïde est alors quelconque et le cristal est biaxe.
Il existe six possibilités pour placer l'indicatrice : chaque indice correspond à un A2 du système.
Position de l'indicatrice dans le système orthorhombique

Position de l'indicatrice dans le système monoclinique
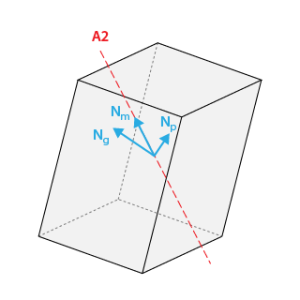
Position de l'indicatrice dans le système triclinique : l'orientation des indices est quelconque
