Minéralogie

Soit une indicatrice avec trois indices différents (ellipsoïde). Prenons la section \(N_p-N_g\) et faisons une rotation de cette section autour de \(N_m\). Comme \(N_m\) a une valeur intermédiaire entre \(N_p\) et \(N_g\), à un moment donné, on a une section circulaire de rayon \(N_m\). On parlera alors de section cyclique^[1].

De par la symétrie de l'ellipsoïde, il existe deux sections cycliques. Les axes perpendiculaires aux sections cycliques sont appelés axes optiques.

Un cristal présentant deux axes optiques est dit biaxe.

L'angle aigu entre les deux axes optiques est appelé (2V). Si \(N_g\) est la bissectrice aigüe de (2V), le biaxe est dit positif ; si c'est \(N_p\), c'est un biaxe négatif.

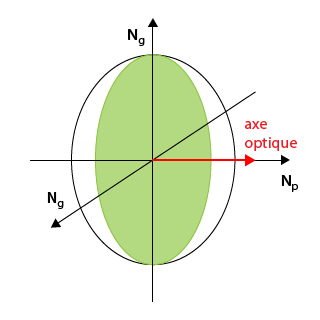
Si deux indices sont égaux, il n'existe qu'une seule section cyclique, donc un seul axe optique. Le cristal est alors dit uniaxe^[2]. Si l'axe est \(N_g\), il est dit uniaxe positif ; c'est l'axe est \(N_p\), il est dit uniaxe négatif.

Si les trois indices sont égaux, l'ellipsoïde est une sphère, il y a alors une infinité de sections cycliques, donc une infinité d'axes optiques. Le cristal est alors isotrope^[3].