Cristaux, symétries et mailles
Définition :
Un minéral est un solide naturel, macroscopiquement homogène, possédant une structure atomique ordonnée et une composition chimique définie quoique variable.
Définition :
Un cristal est souvent repéré par une forme géométrique et la présence de surfaces planes (faces) et d'angles qui se répètent. Cette géométrie traduit ce qu'on appelle l'état cristallin.
Un cristal est un corps caractérisé par l'arrangement ordonné de ses atomes constitutifs. Toutefois, les cristaux ne présentent pas toujours de formes géométriques, simplement parce qu'il n'ont pas eu l'espace suffisant pour les acquérir ; on parle de cristaux xénomorphes[1], par opposition à automorphes[2].
Notions générales
La cristallographie est la science qui étudie les cristaux. Elle diffère de la minéralogie[3], en ce sens que l'état est un état cristallin qui caractérise, outre les minéraux, de nombreuses molécules organiques.
Par opposition à l'état cristallin, on parle d'état amorphe[4] ; il s'agit de matériaux sans arrangement à l'échelle atomique, ce qui se traduit par des formes extérieures toujours quelconques.
Les formes des cristaux ne sont pas quelconques.
Dans les collections de minéraux, il existe des très belles pièces avec des formes bien développées (prismes de quartz, cubes de pyrite, rhomboèdres de calcite, ...).
L'existence de ces formes est liée au fait que dans certains cas, les minéraux ont suffisamment d'espace autour d'eux pour croître et prendre des formes qui leur sont propres. Ces formes macroscopiques traduisent le fait que les atomes sont arrangés à l'échelle microscopique.
Éléments de symétrie
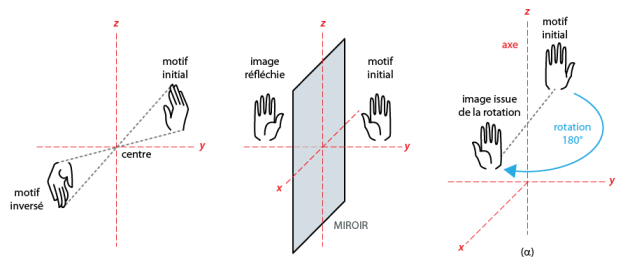
Deux figures sont dites mutuellement symétriques si on peut les faire coïncider par une opération géométrique (transformation géométrique).
Cet opérateur géométrique est appelé "élément de symétrie".
Les éléments de symétrie connus sont :
Elément de symétrie | Notation | Effet |
Point | \(C\) | Symétrie centrale |
Plan | \(M\) | Miroir |
Axe de rotation* | \(A2\) \(A3\) \(A4\) \(A6\) | Rotation de 180° Rotation de 120° Rotation de 90° Rotation de 60° |
Nous pourrons avoir :
la combinaison d'un axe de symétrie d'ordre pair (axe\( A2\), \(A4\) ou \(A6\)) et du centre de symétrie, entraîne celle d'un plan de symétrie, perpendiculaire à l'axe. D'une manière générale, l'existence de deux de ces éléments entraînent l'existence du troisième,
l'existence de deux axes de symétrie \(A2\) entraîne celle d'un troisième \(A2\) perpendiculaire.
Nous appellerons élément de symétrie d'ordre supérieur les axes de rotation strictement supérieur à \(A2\) (c'est-à-dire \(A3\), \(A4\) et \(A6\)). Par conséquent, les éléments \(A2\), \(M\) et \(C\) sont appelés éléments de symétrie d'ordre inférieur.
Notion de maille
Haüy, le grand cristallographe du XIXe siècle a fait une constatation : un cristal fragmenté génère des morceaux qui ont la même forme que le cristal initial (c'est la loi de stratification multiple). Du point de vue géométrique, il existe un certain nombre de volumes de base qui permettent de remplir un espace tri-dimensionnel sans laisser de vides.
Définition :
La maille est l'enveloppe du plus petit parallélépipède de matière cristallisée conservant toutes les propriétés géométriques, physiques et chimiques du cristal et contenant suffisamment d'atomes pour respecter sa composition chimique.
Définition :
Pour construire un volume de cristal, on va en fait empiler des volumes élémentaires ; cette répétition s'appelle le réseau cristallin.
Avant d'aborder les structures tridimensionnelles, nous allons d'abord voir comment remplir totalement un plan.
Cela peut se faire en juxtaposant :
Structure élémentaire : carré
Éléments de symétrie
\(A4~~2A2~~2A'2~~2M~~2M'~~C\)

Modèle

Structure élémentaire : rectangle
Élément de symétrie
\(A2~~A'2~~A"2~~M~~M'~~C\)

Modèle

Structure élémentaire : hexagone
Élément de symétrie : hexagone
\(A6~~3A2~~3A'2~~3M~~3M'~~C\)
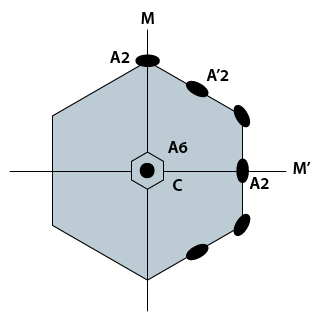
Modèle

Structure élémentaire : losange
Élément de symétrie
\(A2~~M~~M'~~C\)

Modèle

Structure élémentaire : parallélépipède quelconque
Élément de symétrie
\(C\)

Modèle

La géométrie des mailles
La géométrie des mailles fait appel à un primitif, qui est un repère composé de trois axes \(x,y,z\).
L'angle entre ces axes n'est pas forcément de 90° (ce n'est pas systématiquement un repère orthogonal). Sur ce repère, les longueurs \(a\), \(b\) et \(c\) des dimensions du parallélépipéde sont déterminées, mais pas forcément égales.
Chaque maille fait donc appel à 6 paramètres :
trois longueurs : \(a\), \(b\) et \(c\)
trois angles : \(\alpha\), \(\beta\) et \(\gamma\)